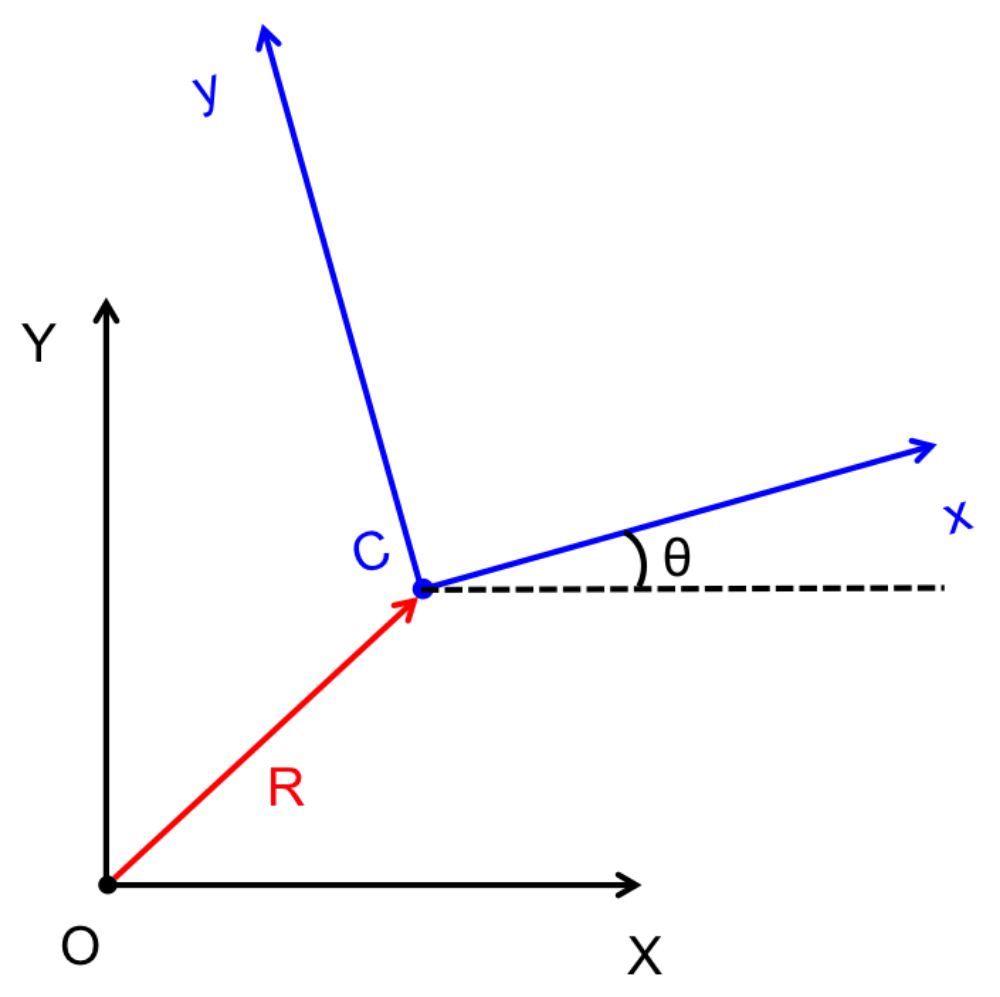
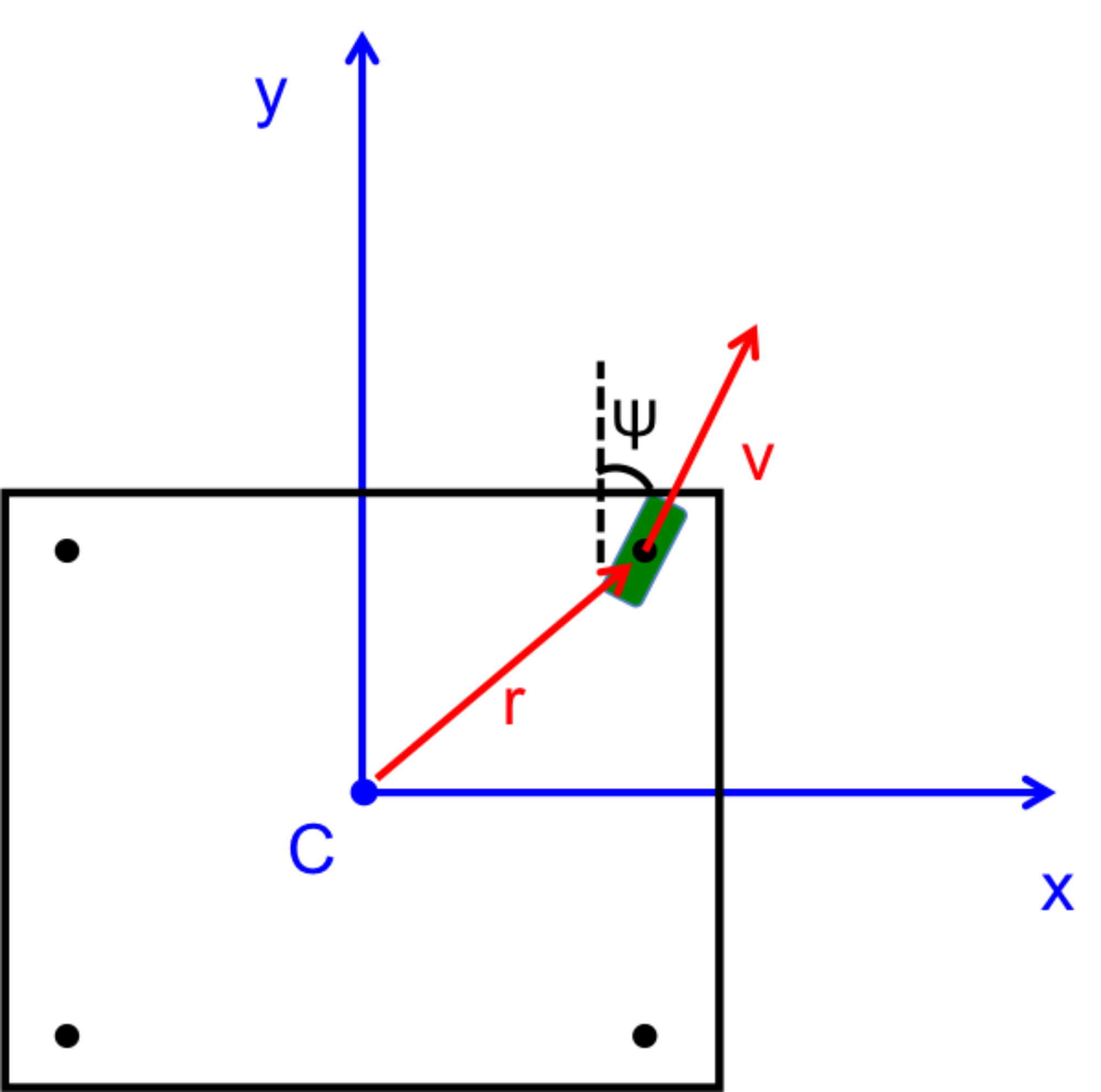
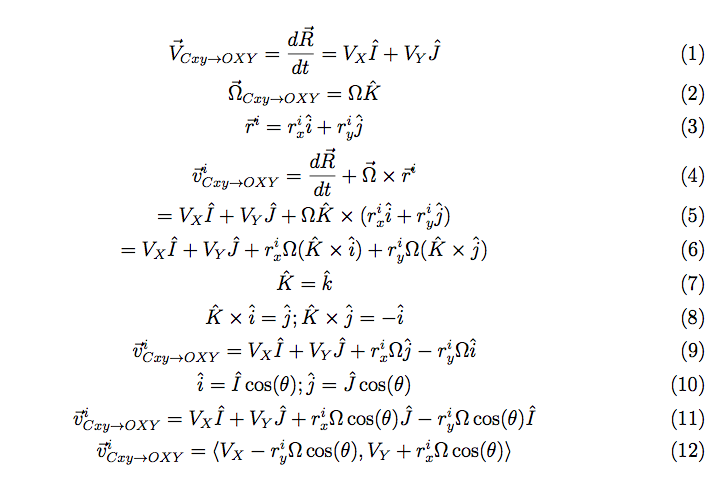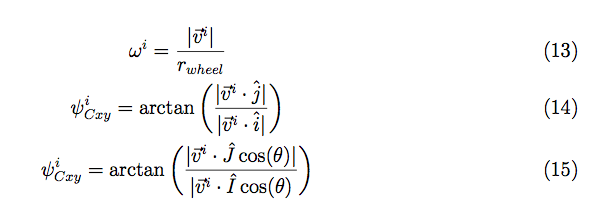Our team finally got the robot moving and steering! Which means it's finally time for me to start the implementation process of the kinematic and control equations. To further verify and help prepare for the implementation, I made a little simulator in MATLAB to help visualize how the robot will move given certain (steady state) commands. Transient commands are a whole other issue, which I may discuss later.
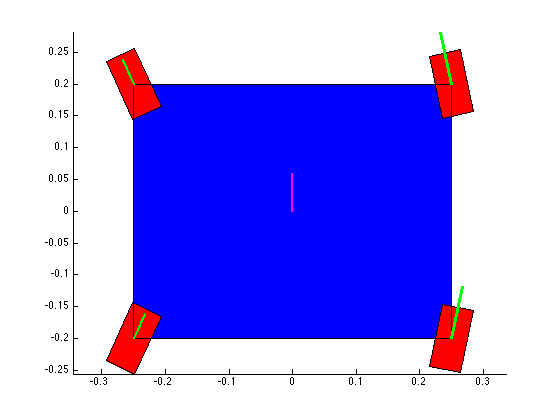
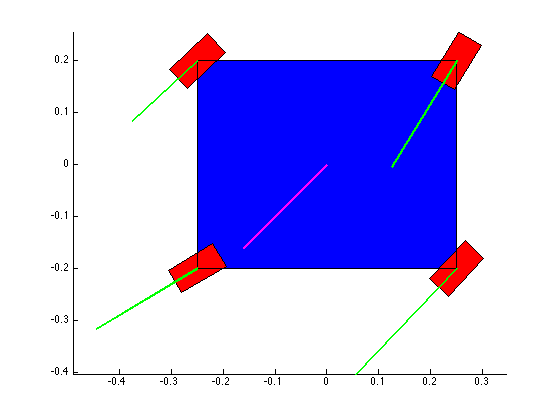
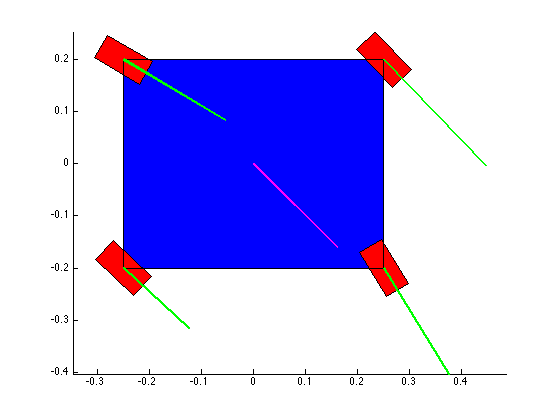
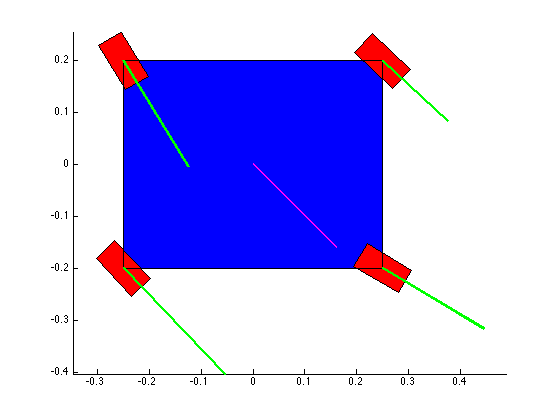
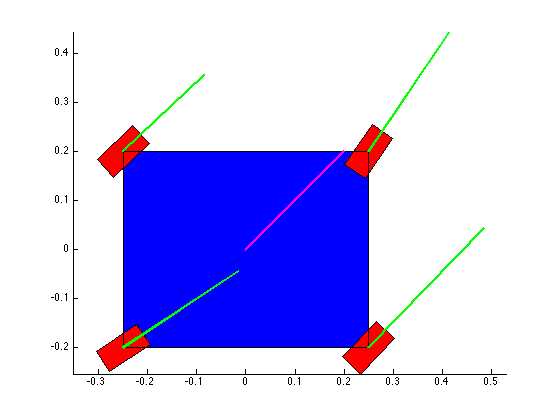
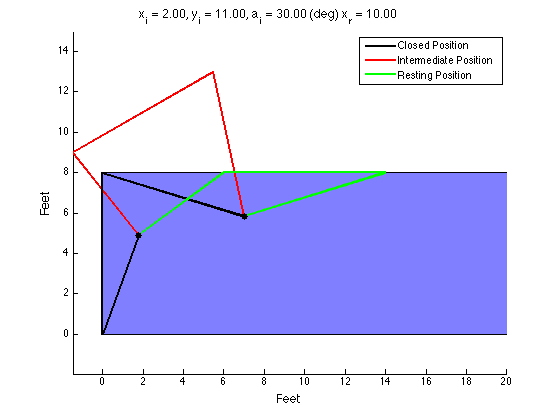
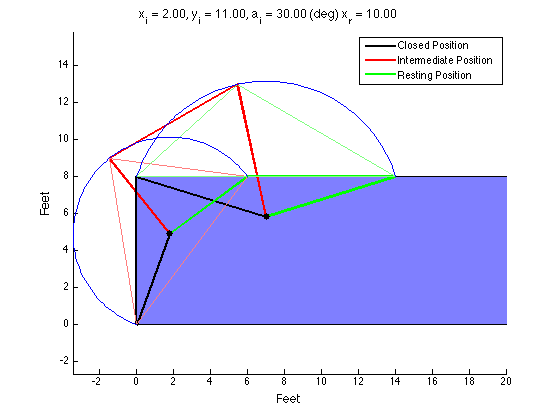
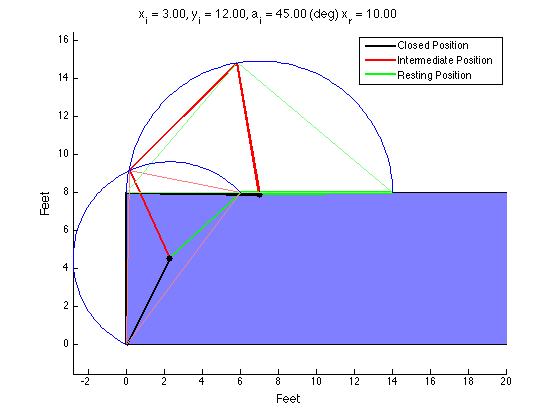
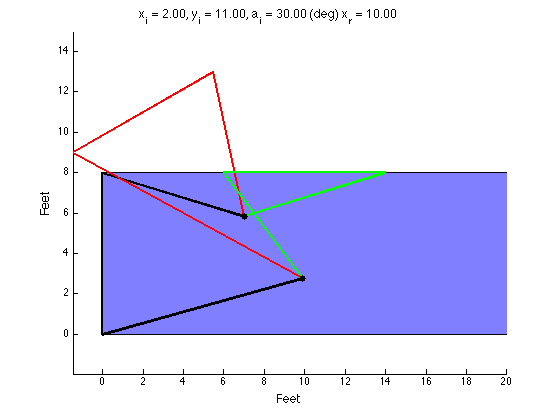
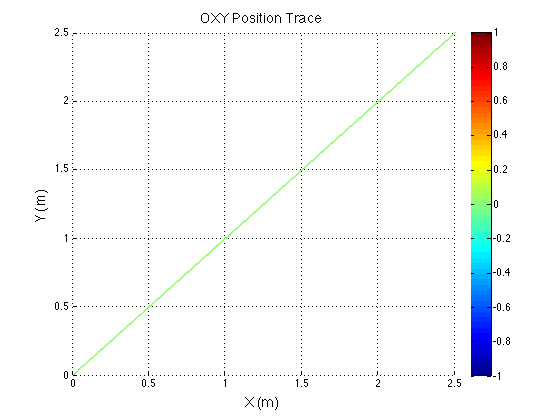
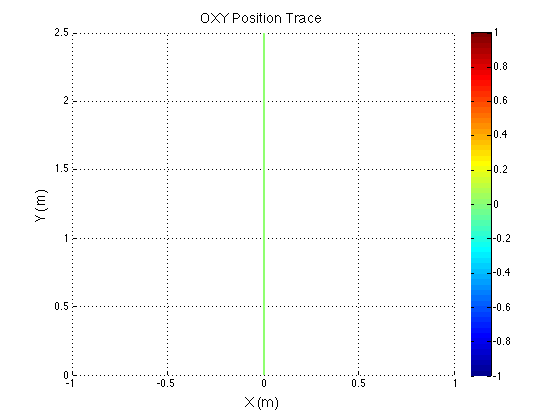
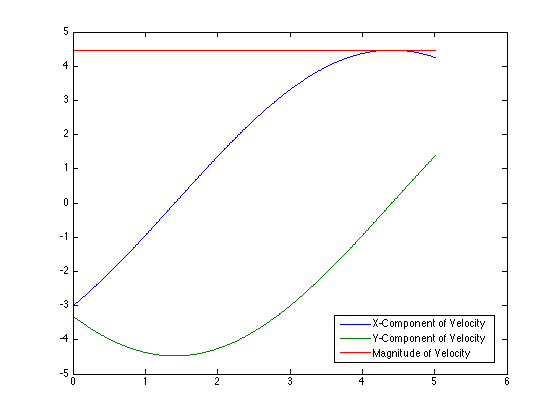
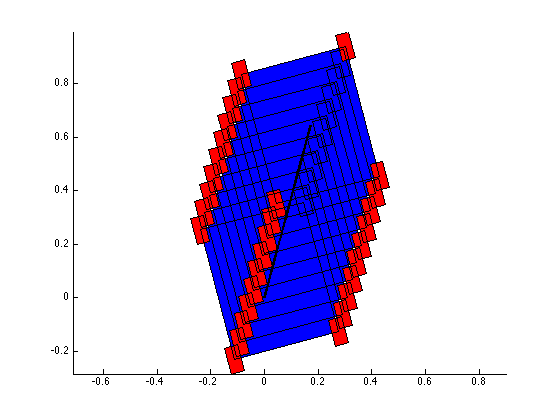
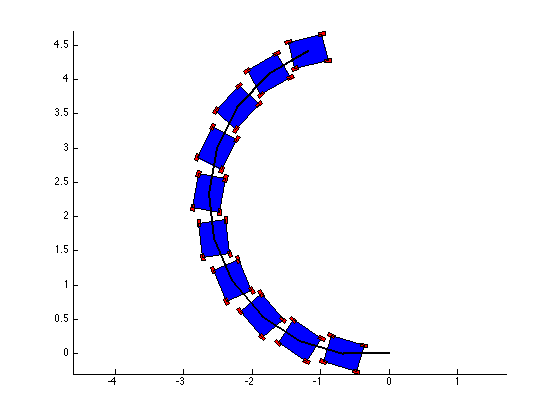
The structure of the top level code is simple. It defines the parameters of the robot and of the simulation, and calls the swerve_command function. This function performs the inverse kinematics and spits out the wheel angles and speeds, as well as the position (x, y, theta) information for that time step. Over several time steps, the robot will move. If steady state inputs are held, the wheel angles and speeds will remain constant, even if the robot itself is executing some curvilinear motion. The robot is plotted at each time step. To verify the wheel angles are correct, you need to visually confirm that the wheels are tangent to the path taken by the wheels in each snapshot.
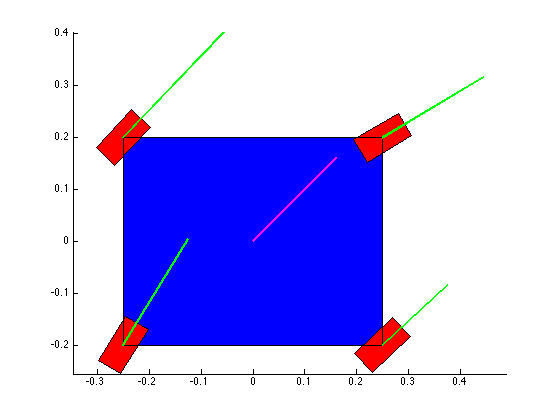
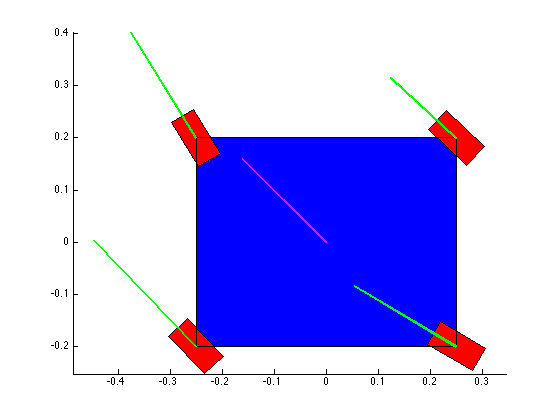
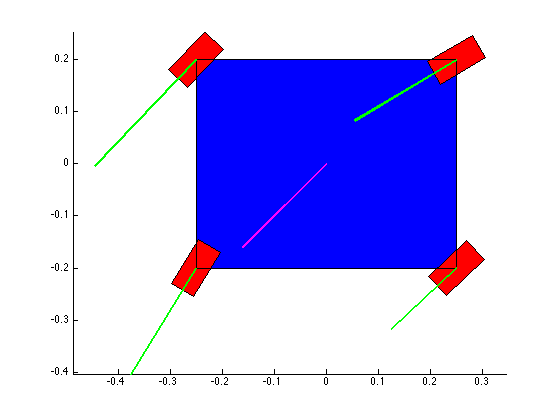
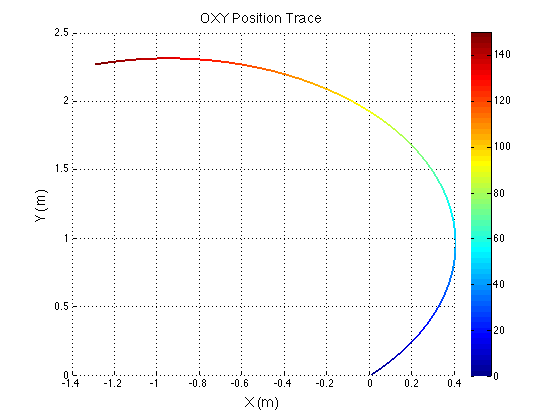
Confirming the wheel speeds is more difficult. For any type of pure translation all the wheel speeds just need to be the same. This has been confirmed. If there is any type of rotation involved, the wheels will orbiting some central point. If the location of the point is known, then the radius to each wheel can be found and using the omega = v/r equation you can confirm that all the angular speeds about that central point are equal. This is hard to do currently because we are normalizing all our speeds because they are simply throttling values which will be sent to the motors. We do not know exactly what speeds they will spin at. However, the ratios of the speeds are telling. What we know is that the wheels on the largest radius of the orbit must have the highest linear velocity, and the wheels on the smallest radius of the orbit must have the smallest linear velocity. This allows all the wheels to have the same angular velocity around that central point. As you can see from the photos, this phenomenon is evident by the colored velocity vectors.
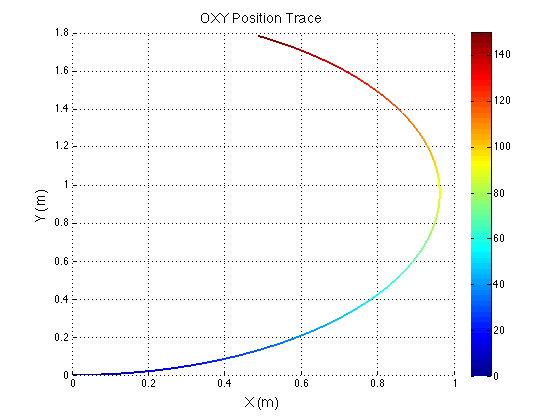
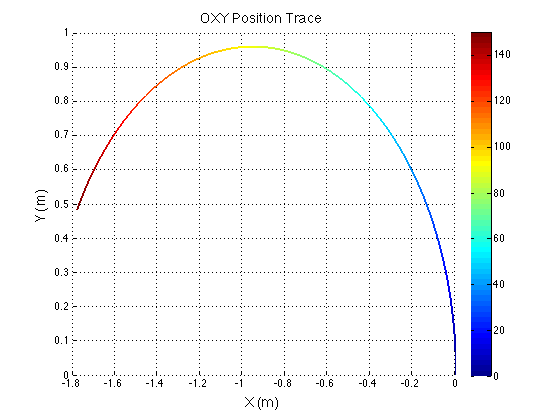
There is something funky going on with the way that the motion of the robot is plotted. The wheel angles and speeds look okay, but when I try to plot the motion some of the components of the motion (X and rotation) have the wrong sign and it looks like the robot is skidding across the floor. I haven't been able to figure out why that is yet. I have a feeling it's some kind of sign error but I haven't found it yet.
Open Issues:
Figuring out how to update the wheel speeds and angles while moving (transient command inputs)
Normalizing the wheel speed outputs to prevent speed commands to the motor from saturating
Finding the little sign errors that are messing things up
Bonus:
We also made a little case for the webcam BreakerBot will be using for the First Person View mode for remote operation. BreakerBot is watching you...

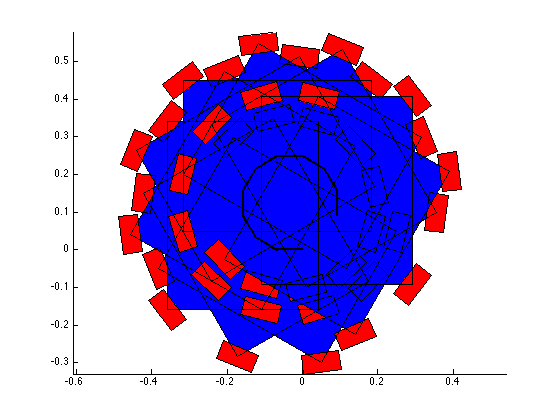

![Here you can see all the wheels have the same velocity [vector] as each other, and as the body of the robot. Bingo.](https://images.squarespace-cdn.com/content/v1/5269e87de4b0f35a9eff7300/1460607019566-W83F44VIT910QGTRMJQY/partial__success3.png)